Category Archives: nRT

nRT

Entre Reaças e Petralhas

Aplicando o sistema eleitoral americano nas eleições brasileiras

BY

Em novembro, os Estados Unidos da América terão sua 58ª eleição presidencial. A nação estadounidense, conhecida por seu fast food de qualidade duvidosa, paixão por armas de fogo e amor à democracia e aos direitos de seus cidadãos tem um sistema de votação complexo e intrincado, funcionando por meio de votos indiretos baseados em colégios eleitorais.

Para entender o negócio todo, talvez a forma mais simples seja transportá-lo à nossa realidade. Como funcionaria se tentássemos adotar o sistema de votação americano no Brasil?

Democratas e Republicanos

O artigo 2 da constituição americana define que os candidatos à presidência devem ter nascido no país, devem ter pelo menos 35 anos e serem residentes estadounidenses por um período não menor do que 14 anos. Os requisitos presidenciais são basicamente os mesmos do que são exigidos por aqui, então não haveriam grandes mudanças nessa área. Mas pode-se dizer que as semelhanças param por aí.

Para adaptar as eleições brasileiras ao formato estadounidense teríamos que jogar fora tudo o que imaginamos sobre partidos políticos. Esqueça essa confusão de 35 partidos, com mais traições do que uma temporada de Game of Thrones, siglas que não representam nada, legendas aleatórias, coligações estapafúrdias, mudanças de lado, partidos corinthianos e posicionamentos inconstantes. A política americana é baseada em dois partidos fortes e uma porção de partidos nanicos que não conseguem grande representatividade e dificilmente irão conseguir.

Da mesma forma como praticamente toda a representação politica em Obamaland pode ser associada com democratas ou republicanos, o similar pode ser aplicado no Brasil, dividindo a grande massa de políticos e eleitores atualmente ativos em dois grandes partidos opostos. Para facilitar a imaginação do leitor, podemos chamar esses dois partidos opostos de reaça e petralha. Isso não quer dizer que esses partidos seriam compostos somente por políticos atualmente afiliados ao PSDB e PT, mas sim às polaridades que esses partidos atualmente representam. Assim, partidos com convicções mais socialistas e progressistas, como PSOL, PCdoB e REDE se alinhariam nas trincheiras petralhas, enquanto partidos de orientação mais liberal e conservadora como PMDB, DEM e PR seriam agregados aos quadros dos reaças (percebam que, por aqui, democratas – DEM – e republicanos – PR – ficam do mesmo lado).

Primárias

Mas como essa enorme divergência de partidos de pensamentos tão distintos podem entrar em um acordo sobre quais candidatos eleger? Se mesmo com o atual sistema, certos partidos têm dificuldades em definir seus presidenciáveis (ou até mesmo os seus prefeituráveis[1]Fiquei imensamente supreso em saber que essa palavra realmente existe: http://www.folhadaregiao.com.br/Materia.php?id=97167), como esse problema se solucionaria em um sistema tão polarizado?

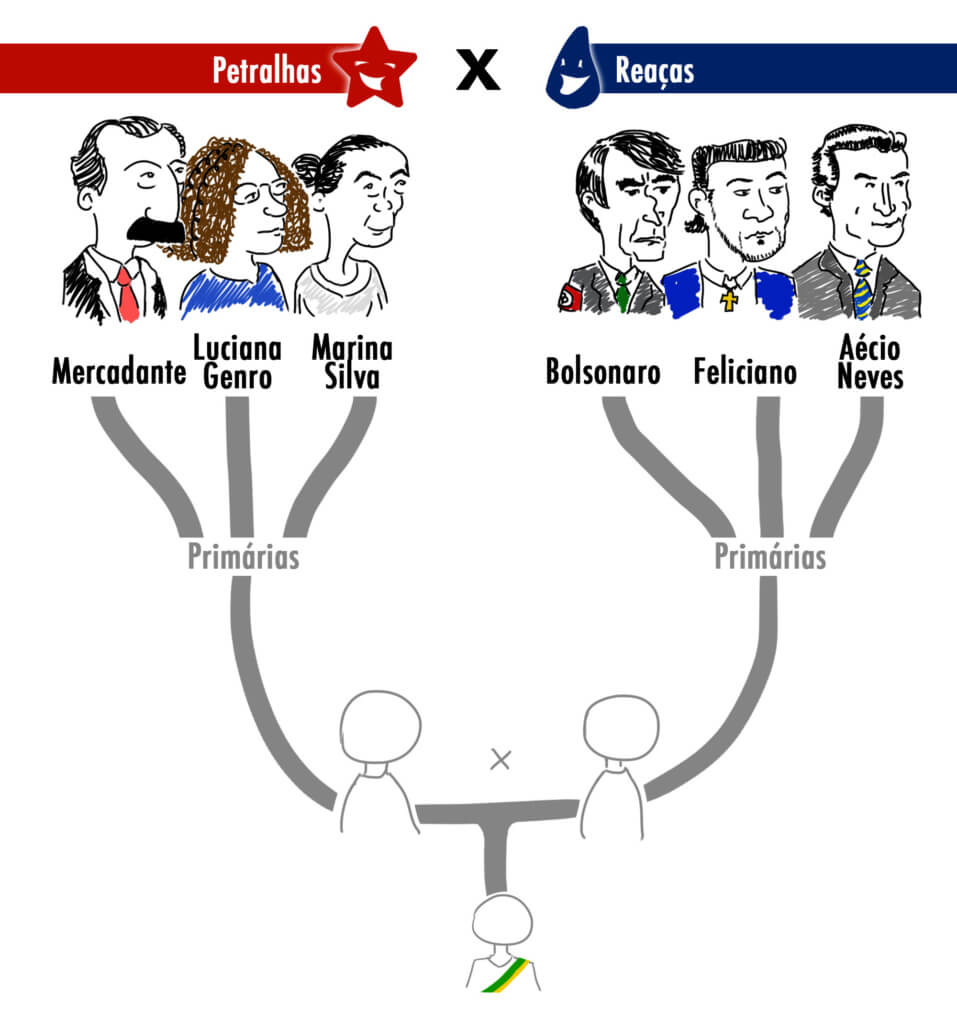
Essa é a idéia das eleições primárias. Nela, petralhas disputariam com outros petralhas e reaças com outros reaças, com o intuito de serem os representantes do partido nas eleições presidenciais finais, aonde apenas dois candidatos participam.

No atual contexto da política brasileira, poderíamos encontrar a seguinte disputa entre petralhas e reaças para as eleições de 2018:

partidos

Há um pequeno detalhe, porém: Em 1947, o Presidente Truman aprovou a vigésima segunda emenda, limitando o número de mandatos que qualquer presidente poderia exercer para apenas dois. Uma das razões seria a idéia de que permitir indefinidos mandatos poderia levar a uma espécie de monarquia. Hillary e Bill poderiam se revezar indefinidamente no poder e a família Clinton nunca deixaria a Casa Branca, por exemplo.

Assim, dois mandatos (podem ser consecutivos ou não) são o limite para qualquer presidente. Isso não só significa que nunca mais teremos os stand-ups do Excelentíssimo Presidente Obama mas também seria o fim da linha para FHC, Lula e Dilma disputarem novas eleições.

Sem a força política de Dilma e Lula, um outro candidato de ideologia parecida deveria entrar na disputa. Talvez, no atual contexto político, as opções mais viáveis seriam Jaques Wagner ou Aloísio Mercadante, ambos já tendo ocupado a cadeira de ministro-chefe da Casa Civil do governo Dilma. Para a chapa Petralha aqui exposta, escolhi Mercadante, pelo simples motivo que seria mais fácil desenhá-lo.

partidos2

Lacra Confirma (Top!)

A votação americana possui regras bem distintas das quais estamos acostumados no Brasil. Pra começar, evidentemente, ninguém é obrigado a ir votar, exatamente como uma democracia deveria ser. Assim, o índice de votações nas primárias é baixíssimo, com apenas cerca de 2

As regras das eleições primárias variam de estado para estado. Nos Estados Unidos há estados que requerem que seus eleitores estejam vinculados ao partido para votar, e outros em que qualquer pessoa pode votar, mas em todos os casos, só é permitido votar em um dos partidos. O processo das primárias não ocorre simultaneamente em todos os estados, se estendendo (no caso deste ano) desde o começo de janeiro até o meio de junho, fazendo as discussões internas dentro dos partidos se prolongarem[2]Eleições primárias americanas por estado: http://www.uspresidentialelectionnews.com/2016-presidential-primary-schedule-calendar/. É um processo longo e chato, que deixaria por mais tempo a timeline do Facebook do cidadão brasileiro mais insuportável do que já é.

Os dois candidatos mais votados de cada partido são os escolhidos para, finalmente, disputar a corrida presidencial. Como é de se esperar, os candidatos derrotados nas primárias declaram apoio ao vencedor de seu partido e a campanha de cada um se estreita. Ao invés do segundo turno das eleições brasileiras atuais, onde há apenas um mês para as idéias dos dois candidatos serem confrontadas, esse processo duraria cerca de quatro meses, com diversos debates, confronto de idéias e, por ser Brasil, envolveria escândalos, troca de acusações, crimes federais e fim de amizades em redes sociais.

As eleições finais ocorrem na primeira terça-feira seguinte à primeira segunda-feira do mês de novembro, um conceito fácil de ser calculado mas que requer ler esta frase ao menos duas vezes para ser entendido.

A votação é feita usando o bom e velho método de papel e caneta, seguido de contagem manual. Os Estados Unidos foi um dos países que recusou o sistema de urnas eletrônicas por considerá-lo inseguro. Ironicamente, são aceitos votos por carta ou por e-mail de cidadãos que moram no exterior. Por conta desse sistema arcaico, a contagem dos votos pode levar dias (vide: Flórida, 2000).

Na segunda etapa do processo o número de eleitores costuma ser bem maior, mas, ainda sem a obrigatoriedade, geralmente ainda fica abaixo dos 5

eleicoes

Tudo ou nada

Uma característica comum às duas fases das eleições, que é certamente a maior diferença em relação ao atual sistema de votação no Brasil é o uso de um voto indireto. Os votos dos eleitores não são diretamente atribuídos aos seus candidatos, mas passam por uma segunda camada de eleição que é conhecida como “delegados eleitorais”. Assim, cada estado possui um determinado número de delegados. E o candidato que possuir mais votos por estado leva os votos de todos os delegados daquele estado – em um sistema chamado “The winner takes it all”; traduzindo: “fode ou sai de cima”.

O estado do Arizona, por exemplo, possui 11 delegados. Se um candidato receber os votos de 5

calculo-peso-eua

No caso americano, o primeiro número é fixo (dois senadores por estado) e o segundo número é proporcional à população. Assim, numa adaptação à República das Bananas, teríamos:

calculo-peso-br

Seguindo essa lógica, o peso de cada estado seria:

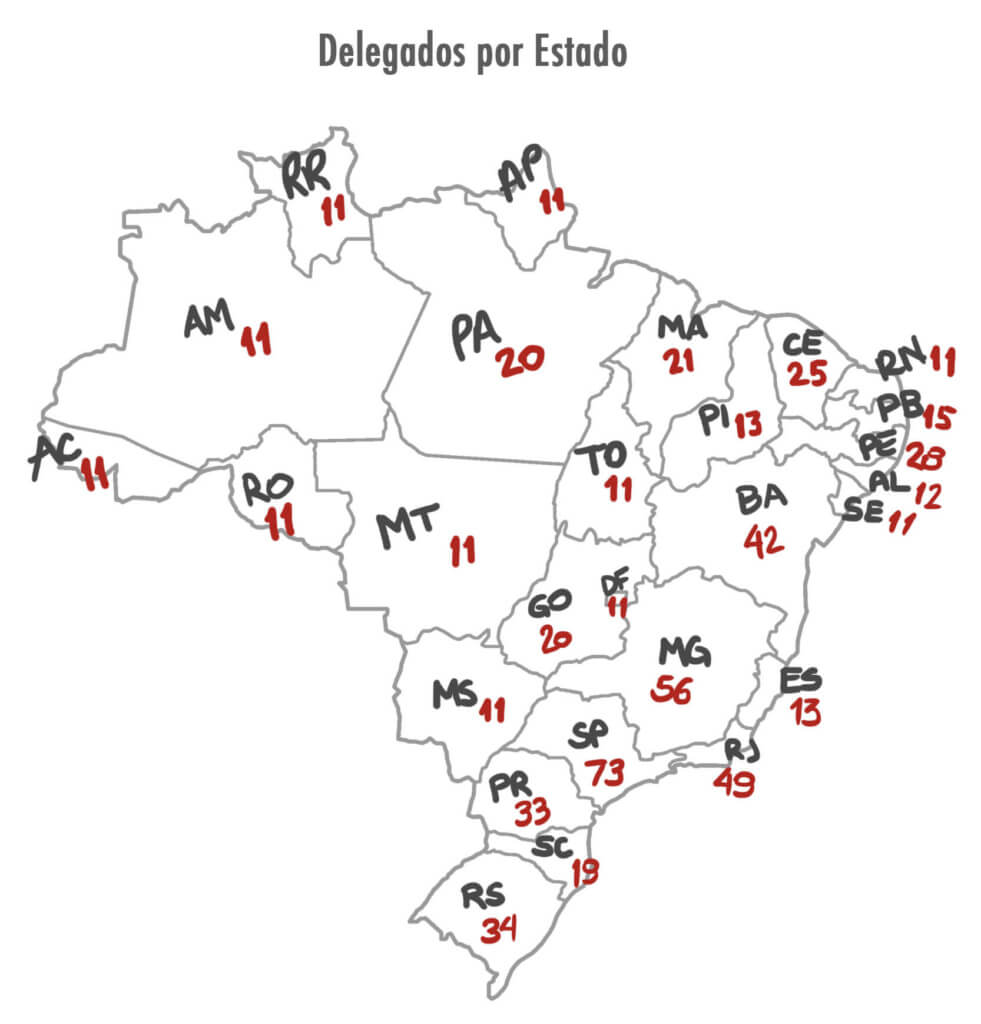
mapa-peso

São Paulo, com sua imensa população tem direito a 70 cadeiras na câmara dos deputados. Somando-se aos 3 Senadores, ele teria 73 delegados e, considerando que, independente da margem de diferença, o candidato que vencesse no estado levaria todos os 73 votos, a disputa das eleições teria uma grande plataforma voltada ao povo paulista. Os estados mais fracos possuem oito cadeiras na câmara e três senadores, portanto o mínimo de cada estado é de 11 delegados.

A maioria simples garante a vitória. Assim, com um total de 594 delegados, o primeiro candidato a obter pelo menos 298 votos é o feliz novo presidente do Brasil.

Teoricamente, os delegados não são obrigados a votar no candidato que se espera deles. Há estados que possuem leis para evitar essa traição e no geral isso não ocorre, então é uma hipótese que não será levada em conta. A eleição do vice-presidente é feita pelos mesmos delegados em dezembro do ano das eleições e novamente eles podem mudar o voto para vice independente do presidente eleito, mas isso também não ocorre, para o alívio do PMDB americano.

Ey-ey-ey-mael

E se os ideais de um político não se encaixam nem com os Reaças e nem com os Petralhas? Apesar da alta cobertura da imprensa ser dedicada quase exclusivamente aos dois gigantescos partidos principais, há uma infinidade de partidos minúsculos nos Estados Unidos que podem entrar na disputa final das eleições. No Brasil, o mesmo ocorreria com determinados partidos, seja por defenderem bandeiras muito extremistas que não teriam representatividade nos partidos maiores, seja em nome de uma maior indepêndencia. Sem contar que qualquer indivíduo pode se candidatar como um candidato independente sem estar filiado a nenhum partido.

Nas eleições brasileiras, esse seria o destino, por exemplo, do PSTU, que provavelmente se recusaria a ser um Petralha. O único partido nanico com alguma representatividade no cenário nacional seria realmente o PV – e essa característica é refletida na política americana, aonde o “green party” é um dos poucos a ser levado a sério fora do eixo Republicano-Democrata.

Sim, porque dentre os outros concorrentes independentes das eleições americanas estão partidos como o “Prohibition Party”[3]Prohibition Party: http://www.prohibitionparty.org/, fundado em 1869 e altamente baseado em ideais cristãos pregando o fim do consumo de álcool ou o Partido “Rent is too damn high”. Essa liberdade toda para qualquer cidadão se candidatar torna as primárias independentes americanas um circo cômico. Em 2016, o criador do Creative Commons se candidatou prometendo que renunciaria após aprovar uma lei para mudar o financiamento de campanha[4]Canidatura de Lawrence Lessig: http://gizmodo.com/meet-the-first-digital-liberties-presidential-candidate-1723497880. Entre outros candidatos bizarros, há John McAfee (sim, do anti-vírus)[5]John McAfee: http://gizmodo.uol.com.br/john-mcafee-jeff-wise/ e Vermin Supreme, que usa uma bota como chapéu e possui uma plataforma de governo que quer tornar obrigatório a todos os cidadãos americanos escovar os dentes, além de financiamento tecnológico para a construção de uma máquina do tempo e promessa de um pônei para cada americano[6]Vermin Supreme: http://www.verminsupreme.com/.

Para conseguir chegar ao ballot final[7]Ballot é o papel de votação onde cada cidadão preencherá o seu voto. Figuram nos ballots apenas os candidatos aprovados de cada partido., os candidatos independentes precisam ter uma votação considerável nas primárias e serem qualificados nos estados. Republicanos e Democratas são automaticamente qualificados (os Reaças e Petralhas também seriam em nosso cenário), porém para os independentes e partidos nanicos, cada estado possui uma regra de qualificação diferente[8]As regras de qualificação variam conforme o estado e podem ser coisas simples como um número mínimo de votos, uma determinada arrecadação de campanha ou fórmulas complexas que levam em conta até eleições passadas dos partidos. As regras são realmente muito complexas e estudá-las pode lhe garantir horas de diversão sanando as próprias confusões aonde você enfiará seu cérebro. Se te interessar saber mais sobre isso, tem esses dois links aqui: https://ballotpedia.org/Ballot_access_for_presidential_candidates e https://en.wikipedia.org/wiki/Ballot_access e nem todos os partidos terminam as primárias com um representante.

Os eleitores sempre têm a última opção que é o “write-in”, aonde eles ignoram todos os candidatos acima e simplesmente escrevem o nome de quem eles desejam votar. Aí residiria a chance de termos Macaco Tião como presidente do Brasil.

Retroatividade

E se as regras americanas fossem válidas já nas eleições de 2014? Considerando que nas primárias a candidata Petralha tenha sido a Dilma Roussef e o candidato Reaça tenha sido Aécio Neves, o método de pontuação de delegados por estado influenciaria no resultado final?

Analisando o resultado obtido por cada candidato por estado:

EstadoDelegadosVencedor
Acre11Aécio Neves
Alagoas12Dilma Rousseff
Amapá11Dilma Rousseff
Amazonas11Dilma Rousseff
Bahia42Dilma Rousseff
Ceará25Dilma Rousseff
Distrito Federal11Aécio Neves
Espírito Santo13Aécio Neves
Goiás20Aécio Neves
Maranhão21Dilma Rousseff
Mato Grosso11Aécio Neves
Mato Grosso do Sul11Aécio Neves
Minas Gerais56Dilma Rousseff
Pará20Dilma Rousseff
Paraíba15Dilma Rousseff
Paraná33Aécio Neves
Pernambuco28Dilma Rousseff
Piauí13Dilma Rousseff
Rio de Janeiro49Dilma Rousseff
Rio Grande do Norte11Dilma Rousseff
Rio Grande do Sul34Aécio Neves
Rondônia11Aécio Neves
Roraima11Aécio Neves
Santa Catarina19Aécio Neves
São Paulo73Aécio Neves
Sergipe11Dilma Rousseff
Tocantins11Dilma Rousseff

Nas eleições de 2014, Dilma venceu em 15 estados, Aécio Neves em 12. Aécio venceu em São Paulo, o que teria lhe garantido o voto dos 73 delegados do estado. Mas mesmo assim, o resultado final ainda seria favorável à candidata petista:

Dilma Rousseff33656.5
Aécio Neves25843.4

Dilma teria a soma de todos os delegados de 15 estados, o que lhe garantiria 336 votos de delegados, o equivalente a 56,5

Por quatro vezes na história o sistema americano já elegeu um candidato que não teve a maioria dos votos do povo, mas que teve uma combinação de votos de delegados suficiente para lhe garantir a vitória. A última vez que isso ocorreu foi em 2000, entre George W. Bush e Al Gore. O candidato democrata teve 50.999.897 votos, contra 50.456.002 do republicano. Porém, os votos de Bush foram suficientes para que ele vencesse em 30 estados, contra 20 de Al Gore, lhe garantindo o voto total de 271 delegados, contra 266 do adversário.

Não é difícil imaginar o mesmo acontecendo no Brasil cedo ou tarde se esse estilo de eleição fosse adotado. Apenas os delegados da região sudeste já seriam o suficiente para garantir a um candidato 191 votos dos 298 necessários. Um candidato que tivesse pouco menos de 5

O atual sistema eleitoral brasileiro parece não ser o culpado pelos péssimos políticos que estamos elegendo. Apesar de idéias que aparentam ser boas, como eleições primárias e, definitivamente, a não-obrigatoriedade do voto, a eleição indireta americana parece menos democrática do que a bagunça gostosa (eu sei, eu sei) que o TSE organiza por aqui.

Se dependesse de mim, porém, as eleições presidenciais não seriam decididas nem por um sistema nem por outro. Eu provavelmente usaria o método do SBT na Casa dos Artistas: colocaria o Silvio Santos numa tarde de domingo telefonando para dez cidadãos brasileiros aleatórios, anotando e influenciando no voto deles. O que eles escolherem, eu aceitaria.

No Abravanel eu confio.

Fontes e referências

Fontes e referências
↑1 Fiquei imensamente supreso em saber que essa palavra realmente existe: http://www.folhadaregiao.com.br/Materia.php?id=97167
↑2 Eleições primárias americanas por estado: http://www.uspresidentialelectionnews.com/2016-presidential-primary-schedule-calendar/
↑3 Prohibition Party: http://www.prohibitionparty.org/
↑4 Canidatura de Lawrence Lessig: http://gizmodo.com/meet-the-first-digital-liberties-presidential-candidate-1723497880
↑5 John McAfee: http://gizmodo.uol.com.br/john-mcafee-jeff-wise/
↑6 Vermin Supreme: http://www.verminsupreme.com/
↑7 Ballot é o papel de votação onde cada cidadão preencherá o seu voto. Figuram nos ballots apenas os candidatos aprovados de cada partido.
↑8 As regras de qualificação variam conforme o estado e podem ser coisas simples como um número mínimo de votos, uma determinada arrecadação de campanha ou fórmulas complexas que levam em conta até eleições passadas dos partidos. As regras são realmente muito complexas e estudá-las pode lhe garantir horas de diversão sanando as próprias confusões aonde você enfiará seu cérebro. Se te interessar saber mais sobre isso, tem esses dois links aqui: https://ballotpedia.org/Ballot_access_for_presidential_candidates e https://en.wikipedia.org/wiki/Ballot_access
nRT

Viajar é preciso

Quanto tempo eu preciso para conhecer o mundo?

BY

Viajar pelo mundo é um sonho comum. Há tanto a se ver, tantos lugares para visitar, comidas para comer, montanhas a escalar, rios a nadar, praias a surfar, florestas para se perder, museus a explorar que uma vida parece pouco para se conhecer tudo. E realmente é. Mas quanto tempo exatamente seria necessário para conhecer o mundo?

Para começar, é preciso estabelecer a primeira definição: Como seria essa viagem? É possível viajar de várias formas, como já descobriram os Beatles em sua fase psicodélica. A forma mais básica e barata de viajar talvez seja simplesmente sair andando por aí.

Método 1: Saia andando por aí

O mundo é um negócio grande. São 510.072.000 km² (ou 5,1×10^8 km², se quisermos usar notações científicas aproximadas, que facilitariam nossas contas). Destes, 149 milhões de km² são de terra e 361 milhões km² de água, sem contar com os 14 milhões de km² da Antartica, que, tecnicamente, deveriam entrar na categoria “água”.

Como não podemos andar sobre as águas (salvo certas exceções[1]inri-cristohttps://nrt.paulovelho.com.br/wp-content/uploads/2016/02/inri-cristo-150x150.jpg 150w, https://nrt.paulovelho.com.br/wp-content/uploads/2016/02/inri-cristo.jpg 450w" sizes="(max-width: 300px) 100vw, 300px" />), então podemos desconsiderar a viagem por mais da metade do planeta. Mesmo porque não haveria muito o que se ver a não ser uma grande imensidão azul molhada.

Não seria preciso também andar por cada centímetro quadrado do planeta. O objetivo é ver de tudo e não pisar em cada pedaço de chão. Assim, podemos definir uma área de visão e, a partir dela, definir quanto seria necessário andar para cumprirmos o objetivo.

Em uma gigantesca planície, um homem de 1,80m consegue enxergar até 5km de distância[2]ver: http://www.livescience.com/32111-how-far-away-is-the-horizon.html e http://blogs.discovermagazine.com/badastronomy/2009/01/15/how-far-away-is-the-horizon. Parece muito pouco – e realmente é. Há outros efeitos a se levar em conta, como a refração atmosférica. No alto de uma montanha, evidentemente seria possível enxergar até centenas de quilômetros de distância, porém, em um vale a visão é reduzida. Outras variáveis, como a neblina ou um amontoado florestal também são limitantes, então, considerando todas as médias, talvez um campo de visão de 5km seja suficiente para nossas contas[3]Sabendo que, quanto mais alto, maior o campo de visão, seria possível economizar alguns dias, aumentando o campo de visão. Pode-se fazer isso andando por aí de salto ou de perna-de-pau, por exemplo..

A velocidade média de caminhada é de 5 km/h. Reservando tempo para dormir, comer e tomar um vinho e um banho e caminhando 9 horas por dia, seriam necessários mais de 900 anos para se andar pelo mundo todo. 46 anos só considerando a Austrália. A idéia básica seria seguir uma linha longitudinal indo e voltando, o que ainda ocasionaria em passar algumas vezes pelo mesmo lugar (para voltar de penínsulas, por exemplo).[4]Com uma perna de pau de dois metros, o raio de visão médio pode chegar a 7,1km e o tempo de viagem pode ser reduzido para 860 anos. Com um zepelin voando a 500m de altura, raio de visão de 80km e velocidade de 14km/h, em pouco mais de 243 anos é possível ter visto o entediante mundo todo.

saia andando…

Seguindo esse algoritmo, só para andar pelo deserto do Saara, seriam necessários mais de 50 anos. Mas também seria possível andar por toda a cidade de São Paulo, com seus 1500 km² em pouco mais de 4 dias, o que não faz muito sentido, já que esse é o tempo apenas para ir de carro de uma ponta a outra da marginal tietê.

Para percorrer áreas urbanas, o campo de visão é limitado. Dessa forma seria melhor definir “conhecer” uma cidade caso você ande por todas as ruas dela. Usando São Paulo como referência, ela possui 17200km de ruas o que, caminhando à 5km/h, nos dá 3440 horas caminhando ou equivalente a 382 dias para conhecer seus 1521km².

Seria equivalente a ter um raio de visão de apenas 44,2 metros; o que parece bastante razoável em uma metrópole onde se estivesse rodeado de prédios, a visão do horizonte ser limitada a algumas dezenas de metros até o amontoado de tijolos mas próximo.

Utilizando o raio de visão de São Paulo como parâmetro, nossa viagem se torna 200 anos mais longa.

Assim, o próprio Matusalem, homem mais velho da história do qual se tem registro (ao menos assim diz a biblia), não conseguiria andar o mundo todo ao longo dos seus 969 anos de vida.

Método 2: Pacotes de viagem

Nem todos nós, porém, temos 900 anos sobrando pra sair andando por aí.

A maioria de nós, na verdade, possui três semanas por ano e ânimo só o suficiente pra comprar um pacote daquela compania de viagens popularesca, de três letras que eu não vou dizer o nome aqui porque eles não responderam meus e-mails.

Eles oferecem um pacote que permite “conhecer” 9 países em 23 dias. Seguindo a lógica, seria possível visitar todos os 196 países do globo em pouco mais de 500 dias. Com 30 dias de férias a cada 335 dias miseráveis de trabalho, uma pessoa conseguiria visitar todos os países em cerca de 25 anos.

Método 3: Proporcional ao número de habitantes

Excursões são um saco e sair andando por aí talvez não seja a forma de viagem mais eficiente. Só para caminhar pelos mais de 9 milhões de km² do deserto do Saara, levaria mais de 57 anos. Como passar 50 anos andando pelo deserto não parece ser o tipo de turismo que agradaria muita gente, eu acabei desenvolvendo um próprio sistema estimativo de viagem.

Após alguns anos viajando por aí, acredito que conheço um pouco sobre viagens. Sei, com alguma experiência, que o tempo necessário para conhecer uma cidade como Londres, com seus 1500km² e quase 9 milhões de habitantes é muito maior do que para conhecer Dar Es Salaam, na Tanzânia, com os mesmos 1500km², mas com menos de 1,4 milhões de habitantes.

A idéia então se baseia no conceito que cidades maiores demograficamente precisam de mais tempo para serem exploradas. Quanto mais pessoas habitam uma cidade, mais coisas há para se conhecer nela. Isso pode ser verdade para Nova York, Londres, San Francisco, Tokio, São Paulo, Buenos Aires e pode não ser tanta verdade para as densamente habitadas Chongqing (China), Dhaka (Bangladesh) ou Lagos (Nigeria). Mas o contrário também pode ocorrer e cidades com pouquíssimos habitantes podem ser tão ricas que seria necessário mais tempo para desfrutá-las, como Te Anau (Nova Zelândia, 1900 habitantes, local dos dois mais lindos e fantásticos fjords do hemisfério sul) ou o Serengeti (um dos maiores parques naturais da África, com 30000km² e nenhum habitante) – sem contar, novamente a Antártida, o único continente com uma população de zero habitantes, mesmo com os governos do Chile e Argentina acusados de enviarem mulheres grávidas para terem filhos no continente nascidos com a nacionalidade antartica.

Na média, a idéia é encontrar um equilíbrio e o tempo desnecessário que seria gasto a mais em cidades populosas e entediantes pode ser usado para compensar as cidades pequenas e incríveis.

O problema básico dessa abordagem é evidente: é impossível conhecer tudo (não que seja realmente possível caminhar 900 anos por aí). Por exemplo: se comêssemos pizza todas as noites em um lugar diferente, seriam necessários 13 anos para termos ido em todas as pizzarias de São Paulo[5]Haja mozzarela: http://noticias.r7.com/economia/noticias/sao-paulo-consome-mais-da-metade-das-pizzas-produzidas-no-brasil-20100710.html.

Seis meses talvez seja um tempo razoável para se dizer que se conhece uma grande metrópole. Nas contas adotadas, qualquer cidade com mais de 5 milhões de habitantes exigiu um período de seis meses de visitação. Talvez não seja o suficiente para metrópoles como Londres e New York, mas honestamente, uma vida não é o suficiente para essas cidades.

Existem hoje 75 cidades com mais de 5 milhões de habitantes. Dentre elas, 18 estão na China. Estados Unidos e Índia agraciam a lista com mais 9 cidades cada um.[6]Demographia. Excelente pdf: http://www.demographia.com/db-worldua.pdf (cuidado: pdf) Considerando o prazo máximo de seis meses, seriam cerca de 40 anos para conhecer as 100 cidades mais populosas do mundo.

Mas cidades populosas são apenas uma pequena fração do que há para ser conhecido. Convenientemente tomando a Alemanha como exemplo[7]Três motivos foram escolhidos para tomar a Alemanha como parâmetro: experiência pessoal de um dos autores (que atualmente mora em Berlim), tamanho do país (por ser pequeno, mas não tanto, é mais fácil fazer as contas) e facilidade em encontrar dados disponíveis (o Brasil infelizmente não possui tantos dados disponíveis sobre suas cidades). E há um motivo extra: porque eu quero.: São 2059 cidades[8]Lista de cidades na Alemanha: https://en.wikipedia.org/wiki/List_of_cities_and_towns_in_Germany (considerando aquelas que possuem uma administração independente), sendo que 16 delas possuem mais de 500 mil habitantes e apenas 3 delas possuem mais de 1 milhão de habitantes. Seguindo a distribuição de viagem por densidade demográfica, seriam quatro meses para conhecer Berlim (o que talvez não seja o suficiente), dois meses para Hamburgo e 34 dias para Cologne (o que seria talvez um exagero). Em dois anos e meio seria possível conhecer completamente todo o país. Fácil se comparado com o Brasil, que dependeria de quase 18,5 anos de turismo.

No total, o mundo todo dependeria de 692,5 anos de viagem para ser conhecido. Um resultado que não foge muito dos 900 anos de caminhada no quesito “impossibilidade”, portanto estranhamente acurado.

Método 4: Desista (ou não)

Se um homem viajasse por 700 anos para conhecer o mundo todo, ao final de sua expedição, o mundo seria diferente do que era quando ele começou. Mais do que isso: as viagens tornaram o homem diferente. Um mesmo homem não sobe a mesma montanha duas vezes, já que o homem que desce é diferente daquele que sobe, porque a montanha muda o homem.

A impossibilidade de conhecer tudo torna a aventura ainda mais empolgante. Sempre há algo novo pra aprender, um novo lugar pra visitar, uma cerveja diferente pra beber, uma experiência diferente para se ter.

Mesmo sabendo que é impossível, a diversão é tentar. Então o melhor a fazer é sair andando por aí logo.

Fontes e referências

Fontes e referências
↑1 inri-cristohttps://nrt.paulovelho.com.br/wp-content/uploads/2016/02/inri-cristo-150x150.jpg 150w, https://nrt.paulovelho.com.br/wp-content/uploads/2016/02/inri-cristo.jpg 450w" sizes="(max-width: 300px) 100vw, 300px" />
↑2 ver: http://www.livescience.com/32111-how-far-away-is-the-horizon.html e http://blogs.discovermagazine.com/badastronomy/2009/01/15/how-far-away-is-the-horizon
↑3 Sabendo que, quanto mais alto, maior o campo de visão, seria possível economizar alguns dias, aumentando o campo de visão. Pode-se fazer isso andando por aí de salto ou de perna-de-pau, por exemplo.
↑4 Com uma perna de pau de dois metros, o raio de visão médio pode chegar a 7,1km e o tempo de viagem pode ser reduzido para 860 anos. Com um zepelin voando a 500m de altura, raio de visão de 80km e velocidade de 14km/h, em pouco mais de 243 anos é possível ter visto o entediante mundo todo.
↑5 Haja mozzarela: http://noticias.r7.com/economia/noticias/sao-paulo-consome-mais-da-metade-das-pizzas-produzidas-no-brasil-20100710.html
↑6 Demographia. Excelente pdf: http://www.demographia.com/db-worldua.pdf (cuidado: pdf)
↑7 Três motivos foram escolhidos para tomar a Alemanha como parâmetro: experiência pessoal de um dos autores (que atualmente mora em Berlim), tamanho do país (por ser pequeno, mas não tanto, é mais fácil fazer as contas) e facilidade em encontrar dados disponíveis (o Brasil infelizmente não possui tantos dados disponíveis sobre suas cidades). E há um motivo extra: porque eu quero.
↑8 Lista de cidades na Alemanha: https://en.wikipedia.org/wiki/List_of_cities_and_towns_in_Germany
nRT

Rios de dinheiro

É possível nadar em dinheiro como o Tio Patinhas?

BY

Resposta rápida e direta: Não.

Mas eu não sou pago para responder perguntas monossilabicamente. Por Deus, eu não sou pago nem pra escrever esses textões pseudo-científicos de gosto e acuracidade duvidosos, mas o faço mesmo assim. Então continue lendo e você vai ver o quão funda é a caixa-forte do pato…

O comportamento de uma criatura pequena em um amontoado de moedas deveria ser mais parecido com o que é visto no filme “O Hobbit” do que os mergulhos ornamentais do pato mais rico de Patópolis.

cartoon

Mas nadar em dinheiro é um sonho tão enraizado no âmago de uma geração que cresceu assistindo Ducktales pelo SBT que matemática hipotética talvez não fosse o suficiente. O ideal mesmo seria testarmos, efetuando o experimento e analisando os resultados.

Para começar, precisaremos saber:

  1. peso do Tio Patinhas
  2. tamanho da Caixa-forte
  3. riqueza contida

1) Um pato normal pesa cerca de 1,5kg. Patos normais não interessam aqui.

Na história de 1963 “For old Dime’s Sake”[1]For old dime’s sake, Carl Barks, 1963: http://coa.inducks.org/story.php?c=W+US+++43-01&pg=1, a Maga Patológica (sério, já pararam pra pensar o quanto esse nome é genial?) mede o Tio Patinhas e conclui que ele possui cerca de 90 cm de altura (ou 3 feet, se formos adotar sistemas métricos sem sentido). Nas proporções humanas, se uma pessoa de aproximadamente 1,80 pesa cerca de 90kg, poderíamos assumir que o peso do pato seria de algo em torno de 45kg. Mas assumir proporções humanas para um pato seria como assumir ideais religiosos em um estado laico, então não devíamos fazer isso.

Para uma alternativa mais realista, precisaríamos saber o peso e altura corretos de um pato fictício. Por sorte, a Marvel mantém um banco de dados público com os detalhes anatômicos de todos seus personagens. [2]Base de personagens da Marvel: http://marvel.com/characters/browse Também por sorte, a Marvel também possui um pato fictício em seu elenco. Comparado com Howard, o pato [3]Perfil de Howard, the duck no site oficial da Marvel: http://marvel.com/characters/981/howard_the_duck, o Tio Patinhas pesaria algo em torno de 20kg, um valor condizente com seus ossos pneumáticos e ausência de calças.

2) Carl Barks, criador do Tio Patinhas e de boa parte de Patópolis descreveu a caixa-forte como “um prédio de aproximadamente 12 andares”. O desenhista Don Rosa, constantemente considerado o herdeiro de Carl Barks nas histórias de Ducktales chegou até mesmo a criar as plantas da construção:

Plantas da caixa-forte por Don Rosa

Plantas da caixa-forte por Don Rosa

Pelas plantas oficiais apresentadas, a caixa-forte teria cerca de 39 metros de altura por 36 metros de lado. É possível ver 12 andares (mais o subsolo) de escritórios, tomando cerca de 9 metros da caixa-forte, restando para o dinheiro um espaço cúbico de 39mx36mx27m.

3) Como calcular a riqueza do pato?

Scrooge-money

Não é como se pudéssemos simplesmente achar o perfil dele entre os bilionários da Forbes…

http://www.forbes.com/special-report/2013/fictional-15/scrooge-mcduck.html

É, esse foi fácil. Com certa freqüência, a Forbes publica uma lista com as mais ricas celebridades fictícias. [4]Forbes Fictional 15: http://www.forbes.com/special-report/2013/fictional-15/index.html De acordo com dados de 2013, Tio Patinhas lidera a lista, com 65,4 bilhões de dólares[5]Perfil de Tio Patinhas na Forbes: http://www.forbes.com/special-report/2013/fictional-15/scrooge-mcduck.html – o suficiente para comprar a Johnson & Johnson ou talvez o Uruguai.

Para o experimento, precisamos:

  1. um pato de aproximadamente 20kg
  2. uma piscina de 39 metros de profundidade
  3. 65 bilhões de dólares.

65 bilhões de dólares (o arredondamento da fortuna do Tio Patinhas custou meros 400 milhões) ocupariam um espaço considerável. De acordo com a teoria de empacotamentos aleatórios, as moedas jogadas aleatoriamente dentro do cofre irão ocupar um volume maior que apenas o volume das moedas somadas, já que haverá espaços vazios entre elas[6]Random close pack: https://en.wikipedia.org/wiki/Random_close_pack http://www.rain.org/~mkummel/stumpers/30jan98a.html.

Tipo de moedaDiâmetro (mm)Espessura (mm)Volume (mm³)Valor unitário (US$)Quantidade necessáriaVolume total (m³)Volume total ocupado (m³) - 6
pennys (1 cent)19,051,52433,230,016.500.000.000.0002.816.026,824.693.378,0312.38
quarters (25 cent)24,261,75808,930,25260.000.000.000210.321350.535,19924,7
moeda de dólar26,4921102,26165.000.000.00071.646,86119.411,4331
um real (câmbio: 3,80)271,951116,480,263247.000.000.000275.771,24459.618,741212,4
ouro (densidade: 19300kg/m³, cotação 34,97 U$/g)26,4921102,26236,8274.489.979302,56504,271,3

[7]Especificações de moedas: http://www.usmint.gov/about_the_mint/?action=coin_specifications https://pt.wikipedia.org/wiki/Moeda_de_um_real

Assim, apesar de possuir uma bem protegida caixa-forte, a fortuna do Tio Patinhas dificilmente se encontra fisicamente toda lá dentro. Boa parte de sua riqueza deve estar investida em suas minas de ouro e ações da Disney.

Assumimos então que apenas um terço de sua fortuna está guardada nos cofres.

Para o experimento, precisamos:

  1. um pato de aproximadamente 20kg
  2. uma piscina de 39 metros de profundidade
  3. 21,5 bilhões de dólares.

Com um peso de 8,1 gramas, uma moeda de um dolar tem a densidade de 7350kg/m³. Com uma ocupação de 6

Um ser humano ou um hobbit, ambos com uma densidade aproximada de 1000kg/m³ também não conseguiria nadar em moedas puras. O sonho de nadar em rios de dinheiro parece mais distante…

O que não quer dizer que não poderíamos ter diversão. Particularmente, com esses recursos em mente, eu tentaria criar a maior piscina de bolinhas do mundo. Pela teoria dos empacotamentos aleatórios, a densidade média de ocupação de esferas gira em torno dos 6

Para o experimento, precisamos:

  1. um homem feliz
  2. uma piscina de 39 metros de profundidade
  3. 169 milhões de bolinhas coloridas

A densidade das bolinhas é de aproximadamente 33,38 kg/m³. Com a taxa de ocupação de 6

Talvez eficaz até demais. Num primeiro instante, o corpo será freado pelo atrito com as bolinhas. Porém, assim que ele tentasse se movimentar (tipo nadar), as bolinhas se moverão, abrindo espaço para descer mais para o fundo. Nadar para cima assim seria tão difícil quanto flutuar no mar da Sícilia com uma bigorna amarrada à perna. Quanto mais movimentos, mais as bolinhas se movimentarão, abrindo espaço para afundar mais rápido, num efeito de areia movediça.

Em pouco tempo, ele atinge o fundo do caixa-forte. Apesar de ter dezenas de metros de plástico acima dele, por serem leves bolinhas, a pressão do ar é apenas ligeiramente mais alta; algo equivalente a estar meio metro debaixo d´água. Mas ele não vai sair de lá. Mesmo que ele organize as bolinhas, empilhando-as para atingir a compactação máxima (7

Porém, melhor fazer isso rápido para não ficar sem ar. O excesso de bolinhas irá impedir uma troca de ar com a superfície. A pouca movimentação de ar que houver será com a tendência de levar o oxigênio para cima, já que expiramos gás carbônico, que é mais pesado que o oxigênio. Andar por todo o fundo do caixa-forte para aproveitar esse ar também não será muito fácil; com a densidade 22 vezes maior que a do ar, o deslocamento será bastante prejudicado. Baixa oxigenação, com alto esforço físico para movimentação não deve acabar bem. À medida que o oxigênio se rarefaz, o esforço para respirar aumenta. Em aproximadamente 5 horas cai-se em uma sonolência profunda seguida de coma[8]Quanto tempo você sobreviveria se fosse enterrado vivo? http://io9.com/heres-how-long-you-can-survive-after-being-buried-aliv-1456805375.

piscina-de-bolinhas

As dicas para quem quiser construir sua própria piscina de bolinhas olímpica é: colocar uma escada e me chamar para brincar nela. E tomem cuidado com crianças. Mesmo para um pato de aproximadamente 20kg como o nosso amigo bilionário, a caixa-forte pode ser uma armadilha mortal.

Talvez até mesmo para um pato convencional (este é o tipo de artigo aonde “convencional” é um adjetivo que faz sentido para um pato) uma piscina de bolinhas seja uma armadilha mortal. Os patos possuem penas impermeáveis (daí que vêm o nome “duck tape”: a fita foi criada para simular as penas dos patos e proteger da água as munições dos soldados durante a guerra[9]Duck tape ou Duct tape? http://www.octanecreative.com/ducttape/duckvsduct.html) e uma glândula uropigial, que produz um óleo que ajuda o pato a flutuar. Isso talvez explique o fato do Pato Donald não usar calças, mas sair do banho com uma toalha enrolada na cintura: é para tirar o excesso de óleo[10]Por que o pato não afunda na água? http://diariodebiologia.com/2010/10/por-que-o-pato-nao-afunda-na-agua. Sem água para boiar, talvez o pato afunde.

Para o experimento, precisamos:

  1. um pato
  2. uma piscina de bolinhas normal

Se alguém puder jogar um pato numa piscina de bolinhas, por favor: filme e me mande o link do vídeo no youtube.

Fontes e referências

nRT

Que a força esteja com você

Como fazer seu próprio sabre de luz em casa

BY

Desde que a galera começou a matar uns aos outros usando pólvora, a arte da esgrima foi destronada de seu propósito militar, sendo hoje utilizada como prática esportiva ou diversão para aquele pessoal nerd que joga action RPG. Os filmes Star Wars, entretanto, trouxeram de volta a luta de espadas, removendo os combatentes de um cenário medieval e colocando em um contexto futurista, com luzes brilhantes auto retráteis que causam um efeito legal nas decapitações.

Com a chegada de um novo filme da franquia, ressurge em nossos coraçõezinhos nerds aquela vontade de ter o sabre de luz próprio, que realizaria nosso sonho de fatiar e torrar o pão simultaneamente.

Aos entusiastas dos trabalhos manuais, podemos tornar esse sonho realidade tão cedo quanto possível. Então pegue a cartolina, o tubo de cola, compre alguns milhares de lasers, descole um buraco negro no eBay e leia nosso pequeno manual de como construir seu próprio sabre de luz!

Lasers!

Lasers são legais pra caramba. São tão legais que é até difícil conceber que eles não passam de um simples feixe de luz, um punhado de fótons se movendo juntos na mesma direção.

No Universo Star Wars, eles são a base de praticamente todo equipamento bélico, das pistolas dos stormtroopers aos raios destruidores de planetas da estrela da morte. É natural imaginar, portanto que nossos sabres de luz sejam compostos por poderosos raios laser.

Até o governo americano está investindo em equipamentos armamentícios. Um laser capaz de derrubar drones [1]Lasers da marinha americana: http://gizmodo.com/5994074/watch-a-navy-laser-gun-blast-a-drone-right-out-of-the-sky já está equipando navios da marinha americana. Uma das principais vantagens de armas laser é o custo de disparo: cada tiro sai por apenas um dólar. Uma pechincha, ainda mais se pensarmos que, em 2000, a Marinha Britânica ganhou o prêmio igNobel da paz por ordenar a seus soldados que, por conta de corte de gastos, ao invés de fazer disparos durante os treinamentos, os oficiais deviam posicionar a arma e um marujo gritaria “BANG” [2]prêmio ignobel da paz para a marinha britânica. http://news.bbc.co.uk/2/hi/uk_news/757788.stm.

nolifeformaboard

A aeronáutica americana também tem planos semelhantes: a idéia é colocar um laser de mais de 100kW em um avião até 2022 [3]lasers em um avião http://breakingdefense.com/2015/05/lasers-on-a-plane-air-force-wants-fighter-firing-100-kilowatts-by-2022/. É potência suficiente para destruir mísseis inimigos e drones, mas talvez não o suficiente para colocarmos em nosso sabre de luz.

Se quisermos arrancar braços e pernas com uma cauterização eficiente de forma a evitar aqueles banhos de sangue de Kill Bill, que poderiam causar curto-circuito nos controles das naves ou tornar o filme impróprio para menores de 16 anos, o sabre de luz teria que evaporar todo o líquido da região com uma profundidade de, digamos, 5 cm. Para uma margem de segurança suficientemente gorda de uma pessoa com uma barriga de 1m de circunferência, o corte transversal resultaria em uma área de aproximadamente 0,07957 m^2. A cauterização de 5 cm de cada lado resultaria num volume de carne e gordura de 0,008 m^3.

Considerando como parâmetro a carne bovina, que possui uma densidade de 1070kg/m^3, esse volume corresponderia a 8,5kg de carne. Com o calor específico de 3,14 kJ/(kg°C) [4]calor-especifico http://jaguar.fcav.unesp.br/lascala/links/Termodinamica03.pdf, seria necessária uma energia de 5187kJ para elevar a temperatura de 36°C a até aproximadamente 230°C (temperatura do óleo fervendo), o que talvez fosse o suficiente para cortar e cauterizar o indivíduo em questão. Considerando que um golpe de sabre leve meio segundo para atravessar o corpo do cidadão (numa estimativa lenta e conservadora), nosso sabre de luz consumiria 10,37MW. Uma lâmpada incandescente, para efeito decomparação, consome 60W.

Um laser comum, daqueles de chaveirinho, usados para entreter gatos possui algo em torno de 5 miliWatts. Seriam necessários mais de 2 bilhões deles, atrás de uma lente convexa para construir nosso sabre de luz. Evidentemente que seria um experimento potencialmente perigosíssimo. Lasers de 1 watt já são poderosos o suficiente para colocar fogo em certos materiais e provocar queimaduras na pele. O que faz parecer extremamente irresponsável a venda liberada destes lasers de 3.5W[5]Wicked Lasers: http://www.wickedlasers.com/ – extremamente propícios para nossa produção manual de sabres de luz, afinal bastariam 3 milhões deles para obtermos a potência necessária para cortarmos o braço do amiguinho. Por 400 obamas cada um, acredito que valha a pena.

sabre_base

A força

Os sabres de luz certamente não são movidos a pilhas. Uma pilha AA tem uma potência de 2.6W. Isso significa que nossa criação gastaria cerca de 4 milhões de pilhas por hora. Seus pais provavelmente não reclamariam mais de comprar pilhas pro carrinho de controle remoto. Uma bateria de iPhone é capaz de fornecer um pouco mais: 8.75W. O que seria o suficiente para abastecer o nosso sabre de luz por um milonésimo de segundo – um pouco de tempo a mais do que ela suporta abastecer um iPhone comum. Cada uma das 20 usinas de Itaipu gera 750MW, então, com um cabo de amperagem suficiente, talvez dê pra ligar o sabre diretamente na rede elétrica.

Para um pouco mais de mobilidade, é possível usar 14 motores V10 de fórmula 1 para abastecer os quase 14000 cavalos de potência que o sabre irá consumir.

sabre_eletricidade

É energia demais até mesmo para os jedis, que produzem a própria força. O Yoda, por exemplo, só consegue produzir 19.2KW [6]How much force can Yoda output? https://what-if.xkcd.com/3/.

Limitadores

Lasers, assim como sitcoms da CBS, não sabem a hora de parar. Nosso sabre de luz teria seu feixe se extendendo pelo Universo, provocando um estrago legal se usado em batalha.

Infelizmente não há nenhuma solução plausível para limitar o alcance da luz emitida pelo nosso punhado de lasers. Não dá pra limitar a luz (ainda), a não ser, talvez com um buraco negro. Buracos negros possuem uma força gravitacional tão intensa que conseguem puxar até a luz e colocar um mini-buraco negro no punhal do sabre talvez venha a ser uma solução para trazer a luz do laser de volta.

Porém, considerando que a luz também é disparada a partir do punhal, talvez o laser nem tivesse força para se extender por alguns centímetros e seja imediatamente sugado pelo buraco negro. Para um sabre de laser caseiro, como o nosso, uma solução talvez seja prender um buraco negro na extremidade de um cabo de vassoura e manter o punhal com o emissor de laser preso na outra extremidade; quando a luz é emitida, ela é sugada pelo buraco negro na ponta, perdendo aquele efeito legal de sabre retrátil, mas mantendo uma aparência bem legal. Fatalmente, o buraco negro acabaria por sugar também os jedis e todo o ambiente em volta, mas seria um efeito bem legal durante os centésimos de segundos que a idéia funcionasse.

sabre_buraconegro

O lado metal da força

Outra característica da luz é que ela não oferece resistência à própria luz. Isso é um problema quando queremos criar aqueles duelos de sabre legais dos filmes, mas é um alívio para todas as outras situações da humanidade.

Para proporcionar duelos plasticamente elegantes e igualmente mortais com nossos amiguinhos do colégio, uma nova abordagem de sabres precisava ser elaborada. Partindo daquele conceito de sabres de brinquedo aonde cilindros de plástico se encaixam uns nos outros e se recolhem no punhal, é possível elaborar uma arma digna de Star Wars. Aplicando uma quantidade ridícula de energia no sabre, é possível fazê-lo começar a liberar fótons e talvez até radiação gama, brilhando numa determinada cor até ficar com aquela aparência de sabre de luz.

Evidentemente que plástico não seria o componente ideal. O brilho começa ser emitido a partir de cerca de 1500°C, com a variação de cor, dependendo da temperatura atingida pelo sabre: [7]Balanço de cores color_balance

Quando um metal é aquecido, seus átomos começam a receber energia. Os elétrons menos energéticos passarão, em forma de onda, para um nível mais energético. Mas ele não consegue se manter por muito tempo nesse nível mais alto e tende a logo retornar ao nível anterior. Para isso, ele deve perder parte da energia que absorveu e ele faz isso em forma de uma onda eletromagnética de determinada freqüência. Quanto mais quente o metal, menor o comprimento da onda desprendida e mais distante do vermelho será a luz gerada pelo sabre. Pelo menos no que diz respeito às cores dos sabres, juntar-se ao lado negro da força parece ser o caminho mais fácil.

Os elementos químicos com os maiores pontos de fusão achados na Terra são o tungstênio (3422ºC) ou o carbono (3527ºC), porém ambos derreteriam antes de chegar na cor azul. Ou seja: só os Sith podem fazer sabres por aqui. Ainda assim seria possível criar sabres sólidos e brilhantes e que certamente cauterizariam seu amiguinho conforme você cortasse o braço dele.

O problema é que o metal também seria rapidamente consumido e o punhal seria provavelmente derretido com tanta energia.

Mesmo sem os efeitos de sabres batendo uns nos outros, lasers cortadores de corpos parecem mais divertidos do que briga com metal semi-derretido. Sem contar que me atrai muito a idéia de uma arma tão mortal, mas que possa ser vencida com um espelho.

Fontes e referências

Fontes e referências
↑1 Lasers da marinha americana: http://gizmodo.com/5994074/watch-a-navy-laser-gun-blast-a-drone-right-out-of-the-sky
↑2 prêmio ignobel da paz para a marinha britânica. http://news.bbc.co.uk/2/hi/uk_news/757788.stm
↑3 lasers em um avião http://breakingdefense.com/2015/05/lasers-on-a-plane-air-force-wants-fighter-firing-100-kilowatts-by-2022/
↑4 calor-especifico http://jaguar.fcav.unesp.br/lascala/links/Termodinamica03.pdf
↑5 Wicked Lasers: http://www.wickedlasers.com/
↑6 How much force can Yoda output? https://what-if.xkcd.com/3/
↑7 Balanço de cores function footnote_expand_reference_container_156_4() { jQuery('#footnote_references_container_156_4').show(); jQuery('#footnote_reference_container_collapse_button_156_4').text('−'); } function footnote_collapse_reference_container_156_4() { jQuery('#footnote_references_container_156_4').hide(); jQuery('#footnote_reference_container_collapse_button_156_4').text('+'); } function footnote_expand_collapse_reference_container_156_4() { if (jQuery('#footnote_references_container_156_4').is(':hidden')) { footnote_expand_reference_container_156_4(); } else { footnote_collapse_reference_container_156_4(); } } function footnote_moveToReference_156_4(p_str_TargetID) { footnote_expand_reference_container_156_4(); var l_obj_Target = jQuery('#' + p_str_TargetID); if (l_obj_Target.length) { jQuery( 'html, body' ).delay( 0 ); jQuery('html, body').animate({ scrollTop: l_obj_Target.offset().top - window.innerHeight * 0.2 }, 380); } } function footnote_moveToAnchor_156_4(p_str_TargetID) { footnote_expand_reference_container_156_4(); var l_obj_Target = jQuery('#' + p_str_TargetID); if (l_obj_Target.length) { jQuery( 'html, body' ).delay( 0 ); jQuery('html, body').animate({ scrollTop: l_obj_Target.offset().top - window.innerHeight * 0.2 }, 380); } }
nRT

Velocidade Máxima Mínima

É possível diminuir o trânsito de uma via diminuindo sua velocidade máxima?

BY

Uma recente decisão da prefeitura de São Paulo desencadeou uma discussão mais política do que científica. A diminuição da velocidade das marginais fez muitos defensores políticos do prefeito tranqüilão irem em busca de justificativas para comprovar a eficácia da medida, em uma atitude extremamente contra-científica, aonde se tem um resultado final e busca-se os experimentos para chegar até ele.

Alguns anos atrás, Doug McDonald, secretário de transporte da cidade de Washington, saiu em uma empreitada parecida, usando arroz e um funil para demonstrar que a diminuição de velocidade faz sentido, num experimento que foi bastante compartilhado. Nele, Doug usa um funil para representar a rodovia e um punhado de arroz como os carros.

Doug McDonald, porém, é formado em direito. É evidente para engenheiros e a turma de exatas que arroz só serve para comer, secar aparelhos eletrônicos e para os formandos em ciências sociais escreverem nomes em grãos nas praias. Doug não está diminuindo a velocidade da via – todos os grãos são movidos pela mesma força de aceleração – mas sim diminuindo o fluxo de entrada. Evidentemente, um fluxo controlado e constante apresenta melhores resultados em situação de gargalo, como qualquer pessoa que já tentou virar uma garrafa de cerveja pode concluir.

Diminuir a velocidade dos carros aumenta a densidade da via. Isso porque um carro a 90km/h precisa de 37m para frear a zero. Levando em conta o tempo de reação do motorista – um ser humano médio que não está acessando nudes no Snapchat – a distância média necessária para o carro da frente passa a ser, no mínimo, 62m. Caso a velocidade seja de 60km/h, essa distância diminui para 42m. Com menor distância entre os carros, maior a quantidade deles na via. Mais carros na via, porém, não significa necessariamente uma melhor fluidez.

Para tirar a prova, decidi construir meu próprio simulador de trânsito, com prostitutas e blackjack: http://nrt.paulovelho.com.br/play/transito/

Cada pixel na tela representa 1,25m. De forma a facilitar o desenvolvimento, apenas três velocidades são calculadas: 30km/h, 60km/h e 90km/h. A distância entre os carros também foi calculada de acordo com a velocidade, sendo de 25m, 50m e 75m respectivamente

O primeiro teste foi feito em condições ideais de trânsito: todos os carros circulando na velocidade máxima permitida da via, respeitando as distâncias, cada um em sua respectiva faixa, com o respectivo amor da vida de cada motorista ocupando o banco do passageiro, em uma quinta-feira, véspera de feriado, saindo do trabalho. Com um fluxo de 8

A explicação é a forma como o fluxo foi calculado: 10

simulador

Mas não vivemos em um mundo ideal: ganhamos menos do que gostaríamos, pesamos mais do que devíamos, nunca estaremos próximos o suficiente da Scarlett Johansson e há trânsito em nossas ruas. Misterioso e incompreensível trânsito por excesso de carros.

O primeiro ponto a ser considerado é: nem todo mundo anda na velocidade máxima da via. Um carro mais lento pode ser o suficiente para causar um gargalo na pista para um motorista impaciente que se esforça para andar o mais rápido possível. No simulador desenvolvido, isso foi facilmente implementado adicionando uma probabilidade do novo carro na pista ser mais lento, variando de acordo com a faixa que ele é adicionado: faixas mais à direita têm mais probabilidade de veículos lentos, tal qual devia ocorrer na vida real.

Mesmo se não houvessem esses veículos mais lentos, o trânsito por fluxo excessivo ainda pode ocorrer graças às chamadas “Shockwave Jams”, que seria um nome muito legal de uma banda de rock. Quando diversos motoristas tentam seguir uma determinada velocidade, mantendo uma determinada distância entre eles, fatalmente, em algum momento uma distração causará uma pequena desnecessária freada em algum deles. Pode ser um espirro, uma chamada no celular ou um pavão que pula em frente ao carro (aconteceu com meu professor de geografia). Essa pequena diminuição causa uma diminuição levemente maior no carro de trás que, por sua vez, propaga para os carros vindouros, espalhando a onda no sentido contrário da via até que, se houver fluxo constante o suficiente, ocasionará em uma parada completa. [1]Shockwave Jams: http://math.mit.edu/projects/traffic/ https://www.newscientist.com/article/dn13402-shockwave-traffic-jam-recreated-for-first-time/

O trânsito causa veículos mais lentos, mas veículos mais lentos não necessariamente causam menos trânsito. Os experimentos de criação de trânsito foram provados a meros 30km/h, seja por universidades japonesas, seja pelos Mythbusters. Em um estudo pela universidade de Stuttgart, na Alemanha [2]Experimental Features of Self-Organization in Traffic Flow: http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.81.3797 , foi feita uma análise da quantidade de trânsito em uma rodovia. Os dados apontam que a faixa da esquerda foi a que apresentou a menor quantidade de trânsito – na Alemanha (e também aqui, teoricamente), as faixas mais à esquerda são destinadas aos carros mais rápidos.

as faixas da esquerda, de velocidades maiores foram as que apresentaram menos trânsito

as faixas da esquerda, de velocidades maiores foram as que apresentaram menos trânsito

O congestionamento é mais dependente do fluxo da via do que da velocidade dos carros; e vias com menor velocidade suportam uma maior quantidade de carros para o mesmo fluxo percentual, dando a idéia de que a diminuição é algo vantajoso. Porém, um alto fluxo resulta naturalmente em uma diminuição da velocidade, sem a necessidade de uma imposição de limites.

Se todos os 8 milhões de automóveis da cidade de São Paulo saíssem ao mesmo de casa e tentassem “entrar” nos 17 mil quilômetros de ruas da cidade (considerando uma média de quatro faixas de rolagem por rua), teríamos pouco mais de 117 automóveis por quilômetro de faixa de rolagem, o que impediria de termos uma velocidade média superior a 8km/h – comprovado pelos filmes de catástrofe e vésperas de carnaval, onde todo mundo tenta fugir da cidade ao mesmo tempo e acaba parado na estrada sem conseguir se mover. Mesmo se apenas 3

Antes de sair postando textão no facebook “toma essa petralhas”, há duas vantagens em uma diminuição de velocidade nas vias. A primeira – e um tanto óbvia – é a diminuição de acidentes. Obviamente, carros mais lentos respondem mais rápido e causam menos acidentes. [3]Departamento de planejamento da cidade de Helsink: http://www.trafikdage.dk/td/papers/papers04/Trafikdage-2004-339.pdf (cuidado: PDF) O maior ganho é na diminuição de atropelamentos, porém uma via como a marginal não deveria esperar o tráfego de pedestres, apesar de estar constantemente apinhada de vendedores de pipoca e trombadinhas bem-treinados.

A outra situação aonde a redução da velocidade máxima da pista influencia na diminuição do trânsito são em casos de gargalos.

Na tese defendida em 2005 pelo professor José Roberto de Godoy [4]Professor José Roberto de Godoy: https://uspdigital.usp.br/tycho/curriculoLattesMostrar?codpes=954679, usando teoria das filas e o software de simulação ARENA (muito melhor e mais acurado do que o meu, obviamente), foi comprovado que uma menor velocidade é capaz de gerar menos congestionamento [5]Controle de Congestionamento Veicular: http://www.ewh.ieee.org/reg/9/etrans/ieee/issues/vol04/vol4issue1March2006/04Castrucci.htm.

O motivo é simples: os carros demoram mais para chegar ao gargalo, causando uma diminuição no fluxo. Alto fluxo é o principal problema dos gargalos, como ficou evidente em outubro, na China, em um congestionamento causado por um gargalo em uma rodovia que diminuía suas 50 faixas (porra, China!) para apenas 20, deixando motoristas presos no trânsito por até 5 dias. [6]Congestionamentos na China: http://www.dailymail.co.uk/news/peoplesdaily/article-3263440/Thousands-motorists-stranded-Beijing-motorway-incredible-50-lane-traffic-jam-week-long-national-holiday-wraps-up.html http://gizmodo.com/heres-the-physics-behind-that-insane-chinese-traffic-ja-1735638335

Porra, Haddad!

Porra, Haddad!

Tomando por base um percurso comum na cidade de São Paulo: As marginais entre a ponte Nova do Morumbi e a ponte das Bandeiras, no sentido sul-norte/oeste-leste – trecho cuidadosamente escolhido simplesmente por ser o caminho que eu costumava percorrer quando saía do trabalho. Na via expressa, há 4 gargalos causados por redução de faixas. O trânsito nas marginais se beneficia com a redução de velocidade especialmente nesses pontos, uma vez que os carros demoram mais para chegar nos trechos problemáticos (e o fluxo é, conseqüentemente, menor).

Mapa de Gargalos da Marginal

Mapa de Gargalos da Marginal

Um outro motivo que a diminuição da velocidade causa menor trânsito é que ela torna as marginais uma opção menos atrativa para se transitar entre dois pontos. Se antes, valia a pena para o motorista perder um pouco de tempo para ir de uma região central às pistas expressas da marginal para poder andar numa velocidade maior – que compensaria o tempo gasto nesse percurso, agora essa via se torna menos atraente, uma vez que o ganho de velocidade nela é pouco vantajoso. Assim, pode ser que a diminuição da velocidade nas marginais cause realmente uma diminuição do congestionamento naquela via, porém pode acabar acarretando também em um aumento no trânsito de vias paralelas ou alternativas.

A solução talvez fosse uma velocidade máxima variável: uma velocidade menor em um horário comercial extendido e velocidade maior nos horários que a via estivesse menos cheia. Ou então, aproveitar que a marginal possui mais de uma via e separar o trânsito: quem for a favor da diminuição de velocidade, que use a via local.

Fontes e referências

nRT

A whole new world

O que aconteceria se Alladin realmente tivesse um tapete voador?

BY

“Alladin” foi o primeiro filme que fui levado a ver no cinema. Eram meados de 1992 e minha falecida tia-avó levou a mim e a meu irmão no antigo cinema da Galeria Olido, no centro de São Paulo.

Na época eu fiquei maravilhado com o personagem do gênio. Eu não queria ter meus desejos realizados, queria só ser amigo daquela criatura azul, engraçada, cheia de poderes e piadas inapropriadas (mas eu nunca tive um amigo assim).

Com o tempo, depois de perder horas preso em engarrafamentos no caótico trânsito da cidade, é que se percebe a utilidade que seria um tapete voador. Não há um porta-malas espaçoso, não pega rádio FM, em dias de chuva é desconfortável, mas é um cacete de um tapete voador veloz e fácil de estacionar.

O tapete tem o ápice de sua participação atuando como wingman do Alladin, quando o personagem principal faz uma visita totalmente invasiva à torre da princesa. Alladin leva um fora, mas a princesa volta atrás quando ele a convida pra dar um rolê no tapete voador, ensinando aos miúdos telespectadores que fica difícil a garota te rejeitar se você tiver um veículo legal. Os dois saem voando no tapete, ao som da balada “A whole new world”, vencedora do Oscar de Melhor Canção Original, em um clipe primoroso.

Não me aborrece o fato do tapete ter capacidades levitacionais ou até mesmo uma consciência fofa. Tudo isso pode ser facilmente explicado pelo argumento “mágica”. Mas é difícil ignorar os efeitos exercidos pela atmosfera terrestre nos personagens, tais como temperatura e pressão.

Com o efeito da rápida subida do tapete da altura da cidade, há uma perceptível diminuição da pressão atmosférica. Os ouvidos do Alladin e da Jasmine fatalmente devem ter tampado. Por isso que a Jasmine canta mais alto.

Conforme eles sobem, o ar também vai ficando mais frio – era melhor a princesa ter levado um casaco. Rapidamente o tapete com os dois pombinhos começa a passar por entre as nuvens.

As nuvens pelas quais eles passam são uma mistura de cumulus humilis com stratocumulus. Essas nuvens fofas, com forma de couve-flor parecem cumulus, e o melhor seria eles voarem para longe dali, porque parece que vai chover. Com o passar da noite, a tendência é que esses cumulus que não chegam a se desenvolver vão ficando menos fofos e mais disformes (transformando-se em stratocumulus). De acordo com dados de temperatura e umidade obtidos do aeroporto de Bagdá, a base das nuvens estava em cerca de 6500ft, ou 1,98km.

Nesse ponto, a turbulência deve ter sido alta, devido às correntes ascendentes do interior da nuvem, então o ideal era que os passageiros estivessem com os cintos afivelados. Em outra imprecisão científica, se tentássemos pegar um pedaço fofo de nuvem em nossos braços como os personagens fizeram, só consegueríamos nos encharcar abraçando um gelado pedaço de nada.

Pouco depois, o tapete voa acima das nuvens. A altura das nuvens pode variar imensamente. Algumas Cumulusnimbus podem chegar até 14km de altitude. Nesse ponto, já na entrada da estratosfera terrestre, a temperatura pode chegar até -60°C. [1]NASA: https://ghrc.nsstc.nasa.gov/amsutemps/amsutemps.pl?r=005

O tapete não chegou tão alto, entretanto. Acima das nuvens eles se deparam com um bando de aves migratórias. Aparentemente são cegonhas, que consegue voar a até 5km de altitude. Mesmo abutres dificilmente passariam de 12km. Na estimativa mais pessimista, podemos assumir que os pássaros são grous comuns mal desenhados, que voam a até 10km de altitude. Tanto cegonhas quanto grous podem ser encontrados voando nos céus da arábia, então não há absurdos geográficos biológicos nas hipóteses exploradas.

Acima de 8km, porém, começa a região conhecida como zona da morte. Nessa altura, o oxigênio é insuficiente para sustentar a vida humana por muito tempo. Aqui, seria conveniente o tapete vir com um sistema automático de máscaras de oxigênio. O Monte Everest chega até 8,848km de altitude, então quando passaram pelo Himalaia (eles passaram, já chegaremos a isso), provavelmente tiveram que contornar alguns picos.

I can show you the world

Hold your breath, it gets better

Considerando a hipótese mais provável, de cegonhas voando a aproximadamente 4500m de altitude, a quantidade de oxigênio disponível já poderia chegar até à metade do que é encontrado à nível do mar, então seria melhor eles pararem de cantar pra segurar o fôlego. Também já seria frio o suficiente para o ar atingir temperaturas abaixo de zero. As partes expostas do corpo da princesa, como os ombros e, especialmente, as extremidades, com as pontas dos dedos e pés, estariam imensamente suscetíveis a queimaduras por congelamento. Jasmine talvez nem percebesse as queimaduras, afinal, inicialmente o efeito delas é dormência e escurecimento da pele na área atingida. O frio deve ser intenso não só por conta da altitude e do passeio ser de noite, mas também devido à alta velocidade do tapete.

 

Altíssima velocidade, aliás.

O tapete percorre um longíssimo caminho, partindo de Agrabah, “cidade de mistério e encantamento”. Mas aonde ficaria Agrabah? Dá pra pegar algumas dicas pelo filme: é uma região desértica e, de acordo com o narrador que conta a história no começo da película, próxima ao Rio Jordão. A arquitetura é típica de um país islâmico, provavelmente Irã ou Arábia Saudita. Tendo esses pontos de referência, minha estimativa pessoal vai para algum ponto da Jordânia. Uma distância aproximada será suficiente para obtermos uma estimativa da velocidade atingida pelo tapete.

Pra começar o passeio, eles sobrevoam a Esfinge de Gizeh, no Egito, a cerca de 500km de distância do ponto de partida. Sem tempo de parar, eles mudam a rota e seguem para o que parece ser a acrópole de Atenas, a cerca de 1120km em linha reta. Por fim, eles vão assistir a uma queima de fogos no telhado do que parece ser um templo da Cidade Proibida na China, a pelo menos 7600 km de distância da Grécia, num trajeto que fatalmente deu a volta pelo Himalaia. O percurso total percorrido dificilmente foi menor do que 9300km.

I can show you the world

I can show you the world

O cálculo da velocidade é bem básico: Distância dividido pelo tempo.

Mas quanto tempo eles levaram nesse percurso?

Se formos considerar o tempo da música, eles levaram 2 minutos e meio – o que nos dá uma velocidade de 62km/s ou 223.200km/h. Ajuda o fato deles estarem indo na direção oeste-leste, que é oposta ao sentido de rotação da terra, assim é possível descontar a velocidade do planeta, de 1675km/h, resultando numa velocidade final de 221.525km/h.

O recorde de velocidade que um ser humano já chegou pertence ao trio de astronautas da missão Apollo 10, cuja cápsula atingiu uma velocidade de 39,897km/h em relação à terra. Alladin e Jasmine podem ter viajado em uma velocidade 5538 vezes maior. Considerando que a velocidade do som é de 1225km/h, eles chegaram na China mais de sete horas e meia antes da música que eles mesmo estavam cantando. É uma idéia totalmente inacurada.

 

Em uma aproximação mais realista, podemos considerar que o passeio todo aconteceu durante uma noite, não apenas durante uma música. Tendo em vista que o ponto mais oeste que o tapete chegou foi no Egito, podemos otimizar a viagem o máximo possível, pegando a noite mais longa da região[2]gaisma: http://www.gaisma.com/, aumentando assim o máximo possível o tempo da viagem. Em uma noite de dezembro, é plenamente plausível o sol se pôr às 17h30 e nascer às 06h30, providenciando treze horas de escuridão. Devemos considerar a viagem de ida e volta, imaginando que todo o passeio ocorreu na mesma noite. Como Egito e Jordânia compartilham o mesmo fuso-horário, a volta deve ter ocorrido ainda no período dessas treze horas.

Considerando seis horas e vinte e cinco minutos de viagem, assim eles mantém um diálogo de dez minutos no topo do templo e retornam ainda na mesma noite. Neste caso, por conta da viagem de volta, não é preciso descontarmos a velocidade de rotação da terra. A velocidade atingida pelo tapete seria de 1453 km/h. O corpo humano é capaz de suportar altas velocidades supreendentemente bem; nosso problema é com a aceleração. A maioria das pessoas costuma perder a consciência entre 4 e 5 Gs de aceleração. [3]Gizmodo: http://gizmodo.uol.com.br/por-que-o-corpo-humano-nao-consegue-suportar-aceleracoes-bruscas/ Mas mesmo se o tapete acelerasse a $$9,806 m/s^2$$ (ou 1G), ele levaria apenas 41 segundos para atingir os 1453 km/h, porém ainda mais lento que a aceleração de um carro de Fórmula 1.

Nessa velocidade, também é plausível começar a levar em consideração o atrito do ar, variável tão desprezada por vestibulandos e engenheiros. O corpo humano não é uma forma devidamente aerodinâmica, nem mesmo a Fernanda Paes Leme. Na altíssima velocidade do tapete, a resistência do ar sobre os passageiros pode significar uma força de quase 2000kg, o equivalente a oito tigres da princesa exercendo um peso contrário ao movimento exercido. Espero que eles tenham segurado firmemente no tapete

Pela altitude atingida, é seguro dizer que o tapete atingiu a velocidade de 1.25 mach; enorme velocidade, mas muito mais coerente, plausível até mesmo para alguns aviões de passageiros supersônicos, como os da companhia Aerion[4]aerion supersonic – http://www.aerionsupersonic.com/, que não patrocina este post, mas devia ter como slogan “Conquiste sua própria Jasmine”.

…ou então podemos levar em consideração aquela teoria de que toda vez que um casal canta um dueto em um desenho da Disney, eles estão fazendo sexo. Aí a balada e o passeio seriam só uma figura de linguagem para representar que Alladin levou a princesa às nuvens. Mas essa seria uma leitura muito resumida. Melhor reservá-la ao pessoal de humanas.

Fontes e referências

Produção Paulo Velho Paulo Velho