Fortnite é o novo jogo do momento que conquistou a moçada. Para quem não conhece essa obra de tiro alternativa da empresa tecnológica Epic®, a premissa é simples: 100 jogadores caem numa ilha na qual uma misteriosa tempestade circular vai se formando, limitando mais e mais a área de jogo. Toda a galera da ilha, ao invés de se unir, formar uma sociedade sustentável e arrumar um jeito de sobreviver à tempestade, vai se matando uns aos outros até que só sobre um jogador, que viverá sozinho para sempre.

A verdade é que toda essa palhaçadinha sem sentido é apenas uma introdução boboca ao verdadeiro propósito deste texto: a verdadeira física por trás do ônibus voador do Fortnite.
Não me incomoda os mistérios da ilha deserta, como os meteoros que os desenvolvedores adicionam a cada temporada ou por que alguém guardaria uma fantasia de arbusto em um baú no sótão de casa. Mas é intrigante a física por trás de um ônibus capaz de voar com um balão de ar quente.
O funcionamento de um balão de ar quente é uma das coisas mais simples da física: o ar de dentro do balão é aquecido e, com isso, suas moléculas se agitam loucamente como suricatos em uma rave. No ar mais frio, as moléculas permanecem mais unidas (provavelmente para se aquecerem). Logo, o ar de dentro do balão se torna menos denso do que ar de fora dele e o balão sobe rápido e alto como a inflação.
Quanto mais quente, menos denso e quanto maior o balão, mais peso ele consegue levantar. Como tudo no Universo, há também uma fórmula matemática para calcular o tamanho que seria necessário para um balão carregar um ônibus. A fórmula mágica é:
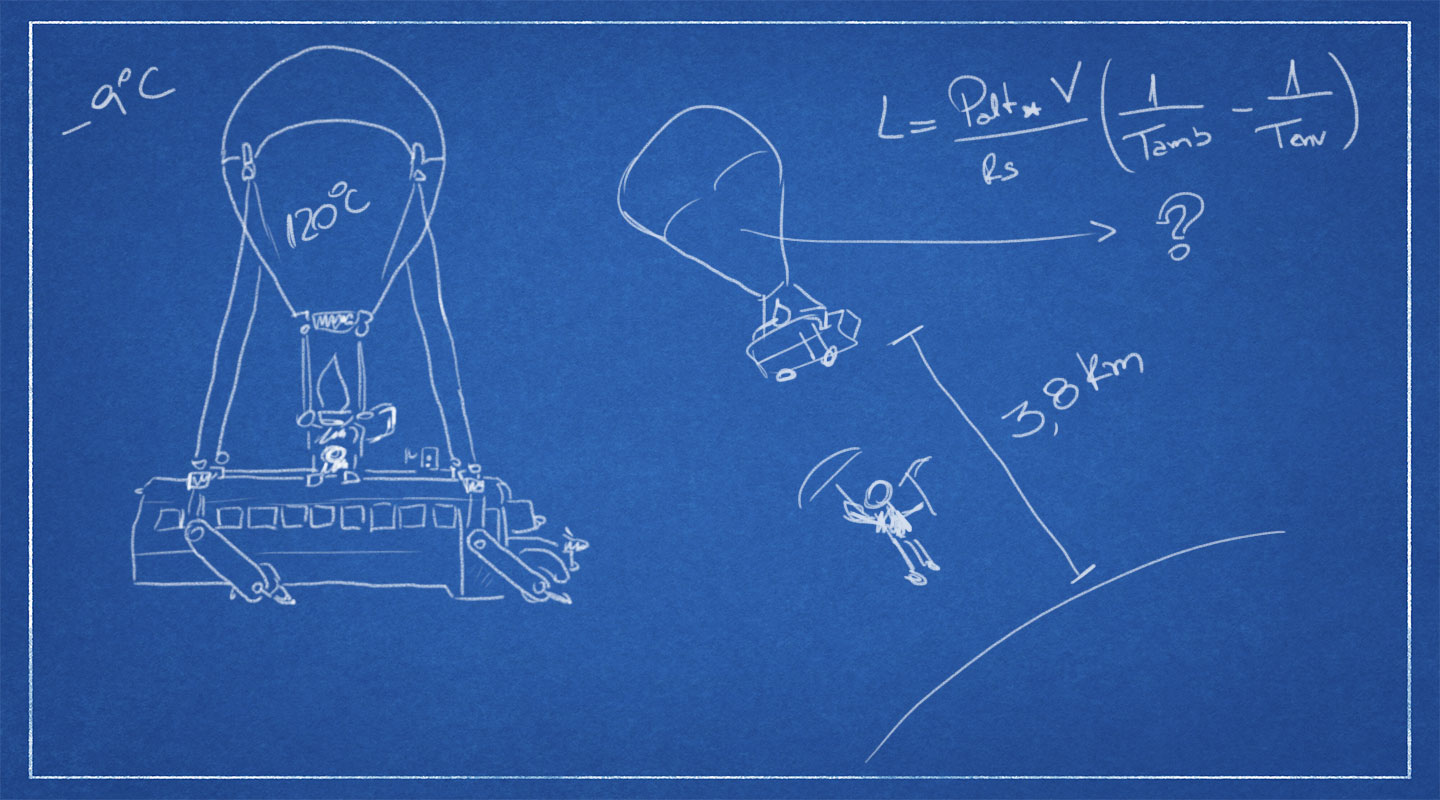
$$! L = \frac{P_{alt} * V}{R_{s}} (\frac{1}{T_{amb}} – \frac{1}{T_{env}}) $$
, onde:
$$L$$ = peso a ser levantado (kg)
$$P_{alt}$$ = Pressão atmosférica na altitude (pascal)
$$V$$ = volume (m³)
$$R_{s}$$ = constante específica do gás (para ar seco: 287.058) ($$J*kg^{-1}*K^{-1}$$)
$$T_{amb}$$ = Temperatura do ambiente (Kelvin)
$$T_{env}$$ = Tempertura do balão (Kelvin)
Peso do ônibus
O ônibus voador usado para transportar os jogadores até o mapa de jogo aparenta ser um ônibus escolar. De acordo com o Google, é possível espremer até 72 crianças dentro de um desses. Conforto claramente não é a prioridade, já que a idéia é tornar o ambiente dentro do veículo tão insustentável que os passageiros aceitem saltar para fora dele munidos apenas de um guarda-chuva e uma picareta. É possível que, sem os bancos, seja possível caber todo mundo.
O peso aproximado de um ônibus escolar é de 12.000kg.
Dentro do ônibus há 100 pessoas (não acho que, dado o propósito do veículo, seja necessário um motorista) que são esbeltas, fortes e caricatas. É justo assumir um peso médio de 75kg por pessoa.
Temos, então 20.000 kg a serem levantados.
Altura de vôo
Para o cálculo da pressão atmosférica e temperatura, é preciso saber a altura de vôo do busão. Como a equipe do Fortnite ignorou meus tweets cheios de perguntas relevantes, tive que calcular essa variável por conta própria.
Após saltar, sem mexer nos controles, o personagem segue em queda livre por 60 segundos. Apesar da aceleração da gravidade, o corpo pára de acelerar quando atinge certa velocidade – é a chamada velocidade terminal. A resistência do ar exerce uma força contrária à da gravidade em qualquer objeto em queda livre. Em determinado ponto, essa força (chamada força de arrasto) se iguala à força da gravidade, cessando a aceleração. A velocidade de queda de um corpo humano em posição deitada (que foi a usada nos testes) é de aproximadamente 55m/s. Sendo assim, o personagem percorre a distância de 3,6km durante essa queda inicial.
Mas não é só isso: depois de uma determinada altura [1]Variável de acordo com a área do mapa aonde o jogador pousa. Nos testes executados, o pouso foi em Loot Lake, no meio do mapa., o personagem abre um pára-quedas (guarda-chuva, no meu caso, já que eu sou um vitorioso) e, cai por mais 21 segundos. Aí o negócio complica: é necessário calcular a nova velocidade de queda. Não há dados consistentes sobre pessoas pulando por aí com guarda-chuvas [2]como tudo nessa vida, é óbvio que alguém já tentou: https://gizmodo.com/5987580/what-happens-when-you-try-to-skydive-with-an-umbrella, com menção honrosa a este chinês estúpido., mas é mais ou menos seguro assumir uma velocidade de queda de aproximadamente 30km/h, levemente mais rápido que os pára-quedas convencionais. São mais 200 metros de queda. Somando tudo, colocando a gordura de erros de cálculo, dá pra imaginar que o ônibus voe a 3,8 km de altitude.
O valor encontrado vai de encontro com o que se é esperado na vida real: A altura padrão de salto de pára-quedas é de 12.000 pés, ou 3,65 km. É uma altitude facilmente atingível pela maioria dos aviões e o saltador não precisa de equipamento especial para oxigênio[3]de acordo com especialistas https://aviation.stackexchange.com/questions/12493/what-is-the-maximum-altitude-a-skydiving-plane-can-fly.
Temperatura e pressão
Não é difícil obter a temperatura e pressão atmosférica em qualquer altitude. Todo piloto e estudante aeronáutico é apresentado a uma tabelinha bem marota chamada “U.S. Standard Atmosphere 1976”[4]esta aqui, ó: http://www.pdas.com/atmos.html, que apresenta os devidos dados de temperatura, pressão e densidade a qualquer altura. A 3,8km de altitude, a tabela nos retorna[5]e eu vou deixar o link para essa calculadora aqui, porque eu tenho certeza que eu vou precisar dela para algum nRT no futuro: http://www.aerospaceweb.org/design/scripts/atmosphere/ o valor de 63,2kPa de pressão e -9,7°C. São dados que mudam dependendo do local do mundo e da época do ano que se está, mas se os pilotos conseguem usar essa base pra pilotar aviões, por deus, eu também posso adotar esses valores para determinar o tamanho fictício de um balão de ar quente gigantesco levando um ônibus computadorizado em um jogo-modinha que nem tem isso como ponto principal do negócio.
A temperatura de dentro do balão, para os nossos propósitos, deve ser a mais quente possível. Os balões de ar quente podem alcançar internamente uma temperatura de 120°C.
Um puta dum balão
Colocando todas as variáveis na fórmula, o volume final do balão seria de 43376m³. Isso dá uma esfera voadora com um raio de 21 metros; um balão da categoria AX-15[6]categorias de balão de ar quente: http://www.hotairballoonrides.com/Hot-Air-Balloon-Sizes.html que teria o dobro do tamanho do atual maior balão do mundo[7]este aqui.

Com esse tamanho e com a absurda potência necessária para aquecer o ar dentro do balão, o ideal mesmo seria adotar um zepelin. O Hindenburg, por exemplo, conseguia transportar até 232 toneladas, também conhecidos como 232000 kg ou 19 ônibus do Fortnite.
E, dado o destino final do Hindenburg, se eu estivesse voando nele, eu não hesitaria em pular de lá levando só uma picareta e um guarda-chuva. Mas eu tentaria formar uma sociedade na ilha ao invés de sair matando todo mundo. Eu tentei algumas vezes no jogo. Não deu certo.
Atualização 2022
Newsletter
Agradecimentos
Mecenas
Zona de cálculo (cuidado: matemática)
Fontes e referências
| ↑1 | Variável de acordo com a área do mapa aonde o jogador pousa. Nos testes executados, o pouso foi em Loot Lake, no meio do mapa. |
|---|---|
| ↑2 | como tudo nessa vida, é óbvio que alguém já tentou: https://gizmodo.com/5987580/what-happens-when-you-try-to-skydive-with-an-umbrella, com menção honrosa a este chinês estúpido. |
| ↑3 | de acordo com especialistas https://aviation.stackexchange.com/questions/12493/what-is-the-maximum-altitude-a-skydiving-plane-can-fly |
| ↑4 | esta aqui, ó: http://www.pdas.com/atmos.html |
| ↑5 | e eu vou deixar o link para essa calculadora aqui, porque eu tenho certeza que eu vou precisar dela para algum nRT no futuro: http://www.aerospaceweb.org/design/scripts/atmosphere/ |
| ↑6 | categorias de balão de ar quente: http://www.hotairballoonrides.com/Hot-Air-Balloon-Sizes.html |
| ↑7 | este aqui |
 Este é meu segundo texto com o título “O busão voador”.
Este é meu segundo texto com o título “O busão voador”.
